Mathematica

für Windows

Eine Arbeit im Rahmen des Mathematik- Unterrichtes der

^{-Berufsmatura}

Autoren:

Anthony Smith, Gümligen

Christian Schlatter, Kaltenherberg

Patrick Strasser, Thun

Über Mathematica

Mathematica ist ein Mathematikprogramm das folgende Bereiche abdeckt:

n Numerische Berechnungen

n Algebraische Operationen

n 2D/3D Funktionen

n Sound

n High-level language Programmierung

n Interaktive Dokumente (Text, Sound, animierte Grafiken)

n Steuern von externen Programmen und Prozessen

1988 wurde die erste Ausgabe für den PC von Wolfram Research herausgegeben. Inzwischen gibt es auch ausgereifte Versionen für Macintosh, SPARC, und UNIX.

Das professionelle Programm wurde für Ingenieure und Hochschulen geschaffen, kann aber problemlos bei einigem Studium auch für den Normalbenützer von grossem Nutzen sein.

Das Programm besteht aus der Arbeitsoberfläche und dem Kernel, dem eigentlichen Rechenprogramm. Die Genauigkeit und Geschwindigkeit der Berechnungen sind stark von der Rechenmaschine abhängig. Für die Version 2.2 ist ein 486er mit 8MB RAM Minimalanforderung, um in einem einigermassen erträglichen Umfeld zu arbeiten. Für die Version 3.0 wird ein Pentium mit 16 MB RAM empfohlen. Das Programm umfasst über 750 eingebaute mathematische Funktionen. Um einfache Umformungs- und Berechnungsaufgaben zu lösen ist das Programm sicher ungeeignet, weil das Programm „einige“ Zeit benötigt um den Kernel zu laden. Um Lösungen grafisch darzustellen oder kompliziertere Aufgaben zu lösen ist dieses Programm sicher eine grosse Hilfe für Jedermann.

Die Oberfläche

Nach dem Aufstarten des Programmes erscheint eine uns vertraute Windows-Oberfläche. Die Grösse, des für den Kernel reservierten Speichers, sollte zu Beginn auf das System angepasst werden. Bei 8MB RAM ist eine Reservation von 10MB empfehlenswert. Die Befehlszeile kann direkt, ohne Vorbereitung, eingegeben werden. Die Eingabe wird mit Shift + Enter abgeschlossen. Beispiel:

In[1]:= ParametricPlot3D 1 [{Sin[t], Sin[2t] Sin[u], Sin[2t] Cos[u]} 2, {t, -Pi/2, Pi/2}, {u, 0, 2Pi} 3, Ticks ->None 4, ViewPoint->{1.300, -2.400, 2.000} 5, PlotPoints->50 6 ]

Die fett gedruckten Zahlen sind für die untenstehenden Erklärungen eingefügt und gehören nicht zur Syntax !

1. Operation

2. Funktion

3. Zahlenbereich der Variablen

4. Grafikanweisungen (hier: kein Überzug)

5. Räumliche Lage der Funktion

6. Auflösung des Variablenbereiches

Out[1]:=ParametricPlot3D

Praktische Anwendungsbeispiele mit Mathematica

Anhand von konkreten Beispielen wollen wir uns einen kurzen Einblick in die ungeahnten Möglichkeiten von Mathematica verschaffen. Damit erhalten Sie die Fertigkeiten im Umgang mit dem Programm und eine Übersicht der Syntax resp. der Philosophie beim verwenden der vielfältigen Befehle. Die Beispiele sind nach Schwerpunkten geordnet. Die 1. Zeile ist die Benutzereingabe; die zweite die Ausgabe des Programmes. Zur Bedienung siehe spezielles Kapitel.

1. Numerische Berechnungen

Beginnen wir ganz einfach...

Auch die grundlegendsten Operationen sind kein Problem!

5 + 7

Mathematica rechnet exakt. Und im Gegensatz zu einem Taschenrechner auch mit grossen Zahlen!

3 ^ 100

515377520732011331036461129765621272702107522001

Der Befehl N liefert Näherungswerte. Will man in der neuen Operation Formeln oder Ergebnisse aus der vorhergehenden verwenden, bietet das Bezugslabel % eine gute Hilfe.

N[%]

5.15378 10⁴⁷

Mathematica rechnet mit jener Genauigkeit, die Sie vorgeben. Die Quadratwurzel aus 10 wird hier auf 50 Nachkommastellen berechnet.

N[ Sqrt[10], 50 ]

3.1622776601683793319988935444327185337195551393252

Mathematica kann auch mit komplexen Zahlen umgehen. I steht hier für die Imaginäre

(3 + 4 I) ^ 10

-9653287 + 1476984 I

2. Grafische Auswertung

Zu den interessantesten Möglichkeiten von Mathematiksoftware wie Mathematica gehören bestimmt die grafischen Funktionen. Mathematica interpretiert alle Grafiken in Postscript, was eine vorzügliche Weiterverwendung in anderen Programmen (Dokumentation) erlaubt oder Ausdrucke auf PS-Druckern vereinfacht.

Mit dem Befehl Plot können jegliche Formeln visualisiert werden. Der Term in den geschweiften Klammern gibt den Wertebereich für x vor.

Plot[ Sin[ Exp[x] ], {x, 0, Pi} ]

Mathematica stellt gute Funktionen zur Verfügung, um die Diagramme zu formatieren. Achsenbeschriftungen, Skalierungen, Wertebereiche und Rasterungen sind sehr einfach zu handhaben.

Show[ %, Frame -> True, FrameLabel -> {"Zeit", "Amplitude"}, GridLines -> Automatic ]

Mit CountourPlot sind Umrissanalysen möglich.

ContourPlot[ Sin [x + Sin[y]], {x, -2, 2}, {y, -2, 2} ]

Sehr interessant ist die Funktion Plot3D, die unter anderem zum „Spielen“ einlädt. Es lassen sich höchst eindrückliche Oberflächenansichten wie die folgende erstellen, die dank der Farbunterstützung speziellen Charakter haben.

Plot3D[ Sin[x + Sin[y]], {x, -3, 3}, {y, -3, 3} ]

Die X-Y-Z-Koordinaten für dieses Gebilde werden als Funktion der Parameter u und t gerendert.

ParametricPlot3D[ {u Sin[t], u Cos[t], t/3}, {t, 0, 15}, {u, -1, 1}, Ticks -> None ]

Oder etwas umfangreicher...

ParametricPlot3D[ {Sin[t], Sin[2t] Sin[u], Sin[2t] Cos[u]}, {t, -Pi/2, Pi/2}, {u, 0, 2 Pi}, Ticks -> None ]

Figuren lassen sich auch zusammenführen:

Show[%, %%]

Einzelne grafische Objekte (hier: Würfel) können im Raum gezielt plaziert werden:

Show[ Graphics3D[ {Cuboid[{0, 0, 0}], Cuboid[{2, 2, 2}], Cuboid[{2, 1, 3}], Cuboid[{3, 2, 1}], Cuboid[{2, 1, 1}]} ]]

Eine sehr spezielle Funktion stellt Play dar: Es lassen sich Wave-Forms generieren, die per Soundkarte abgespielt oder als WAV-Datei gespeichert werden können.

Play[ Sin[1000 / t], {t, -7, 3} ]

3. Algebra

Ein wichtiger Baustein von Mathematica ist zweifellos der Algbra-Teil. Komplexe Formeln lassen sich vereinfachen, umformen, erweitern, analysieren und ausklammern...

Die algebraische Formel...

9 (2 + x) (x + y) + (x + y)^2

9 (2 + x) (x + y) + (x + y)²

Wird mit Expand ausmultipliziert...

Expand[ %^3]

5832 x³ + 9720 x⁴ + 5400 x⁵ + 1000 x⁶ + 17496 x² y + 30132 x³ y +

17280 x⁴ y + 3300 x⁵ y + 17496 x y² + 32076 x² y² + 19494 x³ y² +

3930 x⁴ y² + 5832 y³ + 12636 x y³ + 8802 x² y³ + 1991 x³ y³ +

972 y⁴ + 1242 x y⁴ + 393 x² y⁴ + 54 y⁵ + 33 x y⁵ + y⁶

...mit Factor faktorisiert...

Factor[ % ]

(x + y)³ (18 + 10 x + y)³

Diese Gleichung wird mit Integrate integriert...

Integrate[ x^2 Sin[x]^2, x ]

4 x³ - 6 x Cos[2 x] + 3 Sin[2 x²] - 6 x Sin[2 x]

...mit D differenziert...

D[ %, x ]

12 x² - 12 x² Cos[2 x]

... und mit Symplify vereinfacht:

Simplify[ % ]

x² Sin[x]²

4. Gleichungen auflösen

Gleichungen aufzulösen ist vielfach ein arbeitsaufwendiges Prozedere. Gerade bei grösseren Problemen erweist sich der PC hier als guter Arbeitskollege.

Die kubische Gleichung wird zuerst neu sortiert:

x^3 -7 x^2 + 3 a x == 0

3 a x - 7 x² + x³ == 0

Und schliesslich in die drei Lösungen für x zerlegt

Solve[ %, x ]

{{x -> 0}, {x -> 7 - Sqrt[49 - 12 a]}, {x -> 7 + Sqrt[49 - 12 a]}}

2 2

Ebenso verläuft der Prozess bei Gleichungssystemen: (Man beachte die Doppel-=)

Solve[ { a x + b y == 0, x + y == c } , {x, y} ]

a c a c

5. Listen und Wertepaare

Hat man beispielsweise eine Tabelle und will mit diesen Werten jeweils die selben Operationen durchführen, eignen sich sogenannte Tables und Arrays.

Hier erstellen wir eine Tabelle mit den ersten 15 Fakultäten

Table[ n!, {n, 1, 15} ]

{1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800,

479001600, 6227020800, 87178291200, 1307674368000}

Aus diesen obigen Werten bilden wir eine neue Wertetabelle, welche die Logarithmen der Fakultäten enthalten. N errechnet Näherungswerte.

N[ Log[ % ] ]

{0, 0.693147, 1.79176, 3.17805, 4.78749, 6.57925, 8.52516, 10.6046,

12.8018, 15.1044, 17.5023, 19.9872, 22.5522, 25.1912, 27.8993}

Diese Werte können nun im Koordinatensystem dargestellt werden:

ListPlot[ % ]

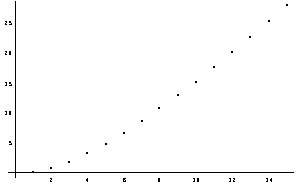
Mit Fit sucht Mathematica eine quadratische Gleichung, die diesen Werten am nächsten kommt.

Fit[ %2, {1, x, x^2}, x ]

-1.48508 + 0.963131 x² + 0.06766 x

Mit dieser Anweisung wird ein zweidimensionales Array mit der Ausdehnung 30 x 30 erstellt und mit binären Werten gefüllt.

array = Table[ If[GCD[i, j] == 1, 1, 0], {i, 30}, {j, 30} ] ;

Mit ListDensityPlot wird nun dieses Array aufgerollt und der Inhalt grafisch dargestellt.

ListDensityPlot[array]

6. Matrizen

Die Matrizenrechnung nimmt in der höheren Mathematik eine sehr wichtige Stellung ein. Gerade in der Stochastik ist Mathematica ein gutes Werkzeug.

M generiert eine Matrix, die Mathematica als Listen einer Liste ausgibt.

m = Table[ 1 / (i + j + 1), {i, 3}, {j, 3} ]

1 1 1 1 1 1 1 1 1

{{-, -, -}, {-, -, -}, {-, -, -}}

3 4 5 4 5 6 5 6 7

Die Matrize kann invertiert werden.

Inverse[ m ]

{{300, -900, 630}, {-900, 2880, -2100}, {630, -2100, 1575}}

Multiplizieren wir die ursprüngliche Matrix mit der Inversen.

% . m

{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}

Erstellen wir eine neue Matrix mit einer geänderten Führungsdiagonalen

m - x IdentityMatrix[3]

1 1 1 1 1 1 1 1 1

{{- - x, -, -}, {-, - - x, -}, {-, -, - - x}}

3 4 5 4 5 6 5 6 7

Die Determinante liefert ein charakteristisches Polynom der Matrize

Det[ % ]

1 317 x 71 x 3

------ - ----- + ----- - x

378000 25200 105

Eigenvalues berechnet die Eigenwerte der Matrix direkt

Eigenvalues[ N[ m ] ]

{0.657051, 0.0189263, 0.000212737}

Dieser Befehl berechnet die Eigenwerte aus einer 100x100 Matrize aus Zufallszahlen.

Das Semikolon am Schluss unterdrückt die Protokollierung.

Eigenvalues[ Table[Random[ ], {100}, {100}] ] ;

Nun können wir den Sachverhalt noch grafisch darstellen!

ListPlot[ Transpose[ {Re[%], Im[%]} ] ]

7. Rechnen mit Platzhaltern und Symbolen

Komplexe Probleme erfordern häufig die Anwendung von Platzhaltern für grössere Zahlen und Formeln. Mathematica stellt hier grosse Möglichkeiten zur Vereinfachung zu Verfügung.

Aus den drei Gliedern a, b und c berechnen wir die 6 Möglichen Permutationen

Permutations[{a, b, c}]

{{a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, {c, b, a}}

Flatten fügt die einzelnen Terme zu einem zusammen

Flatten[ % ]

{a, b, c, a, c, b, b, a, c, b, c, a, c, a, b, c, b, a}

Nun können wir alle Positionen von b aufspüren

Position[ %, b ]

{{2}, {6}, {7}, {10}, {15}, {17}}

Häufungsprodukte der Positionen

FoldList[Times, {1}, %]

{{1}, {2}, {12}, {84}, {840}, {12600}, {214200}}

Erstellen wir eine Liste von verschachtelten Cosinus-Funktionen...

NestList[ Cos, x, 3 ]

{x, Cos[x], Cos[Cos[x]], Cos[Cos[Cos[x]]]}

...und stellen diese graphisch dar.

Plot[Evaluate[%], {x, 0, 1} ]

8. Mathematica Add-Ons (erweiterbar)

Mathematica enthält verschiedene Zusatzpakete für Spezialgebiete. Diese Zusatzpakete sind programmier- und erweiterbar.

Die << laden ein solches Add-On. Hier das Modul über Chemische Elemente.

<<Miscellaneous`ChemicalElements`

Beispielsweise ist das Atomgewicht des Elementes Tungsten eruierbar

AtomicWeight[Tungsten]

183.85

Bei Plutonium erhalten wir die Warnung, dass keine stabile Isotope vorhanden sind (radioaktiv)

AtomicWeight[Plutonium]

AtomicWeight::unstable: No stable isotope of Plutonium exists.

244

Off verhindert solche „Fehler“-Meldungen

Off[AtomicWeight::unstable]

Dieser Plot zeigt das Verhältnis des Atomgewichts zu den Anzahl Elektronen

ListPlot[ AtomicWeight[Elements]

/ AtomicNumber[Elements], PlotJoined -> True ]

Lädt das Geometrie-Paket und zeigt eine Ansicht eines grossen Ikosahedron

<<Graphics`Polyhedra`

Show[ Polyhedron[GreatIcosahedron] ]